analysis

MRS.analysis

Analysis functions for analysis of MRS data. These include a variety of functions that can be called independently, or through the interface provided in MRS.api.

bootstrap_stat

MRS.analysis.bootstrap_stat(arr, stat=<function mean at 0x106a0d500>, n_iters=1000, alpha=0.05)

Produce a boot-strap distribution of the mean of an array on axis 0

arr : ndarray

The array with data to be bootstrapped

stat : callable

The statistical function to call. will be called as stat(arr, 0), so needs to accept that call signature.

n_iters : int

The number of bootstrap iterations to sample

alpha : float

The confidence interval size will be 1-alpha

coil_combine

MRS.analysis.coil_combine(data, w_idx=[1, 2, 3], coil_dim=2, sampling_rate=5000.0)

Combine data across coils based on the amplitude of the water peak, according to:

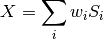
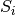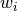Where X is the resulting combined signal, are the individual coil signals and are calculated as:

Parameters:

data : float array

The data as it comes from the scanner, with shape (transients, echos,

coils, time points)

w_idx : list

The indices to the non-water-suppressed transients. Per default we take

the 2nd-4th transients. We dump the first one, because it seems to be quite different than the rest of them...

coil_dim : int

The dimension on which the coils are represented. Default: 2

sampling rate : float

The sampling rate in Hz. Default : 5000.

fit_gaussian

MRS.analysis.fit_gaussian(spectra, f_ppm, lb=2.6, ub=3.6)

Fit a gaussian function to the difference spectra to be used for estimation of the GABA peak.

Parameters:

spectra : array of shape (n_transients, n_points)

Typically the difference of the on/off spectra in each transient.

f_ppm : array

lb, ub : floats

In ppm, the range over which optimization is bounded

fit_lorentzian

MRS.analysis.fit_lorentzian(spectra, f_ppm, lb=2.6, ub=3.6)

Fit a lorentzian function to spectra

This is used in estimation of the water peak and for estimation of the NAA peak.

Parameters:

spectra : array of shape (n_transients, n_points)

Typically the sum of the on/off spectra in each transient.

f_ppm : array

lb, ub: floats :

In ppm, the range over which optimization is bounded

fit_two_gaussian

MRS.analysis.fit_two_gaussian(spectra, f_ppm, lb=3.6, ub=3.9)

Fit a gaussian function to the difference spectra

This is useful for estimation of the Glx peak, which tends to have two peaks.

Parameters:

spectra : array of shape (n_transients, n_points)

Typically the difference of the on/off spectra in each transient.

f_ppm : array

lb, ub : floats

In ppm, the range over which optimization is bounded

fit_two_lorentzian

MRS.analysis.fit_two_lorentzian(spectra, f_ppm, lb=2.6, ub=3.6)

Fit a lorentzian function to the sum spectra to be used for estimation of the creatine and choline peaks.

Parameters:

spectra : array of shape (n_transients, n_points)

Typically the sum of the on/off spectra in each transient.

f_ppm : array

lb, ub : floats

In ppm, the range over which optimization is bounded

get_spectra

MRS.analysis.get_spectra(data, filt_method={'filt_order': 256, 'lb': 0.1}, spect_method={'BW': 2, 'NFFT': 1024, 'n_overlap': 1023}, phase_zero=None, line_broadening=None, zerofill=None)

Derive the spectra from MRS data

Parameters:

data : nitime TimeSeries class instance or array

Time-series object with data of shape (echos, transients, time-points), containing the FID data. If an array is provided, we will assume that a sampling rate of 5000.0 Hz was used

filt_method : dict

Details for the filtering method. A FIR zero phase-delay method is used with parameters set according to these parameters

spect_method : dict

Details for the spectral analysis. Per default, we use

line_broadening : float

Linewidth for apodization (in Hz).

zerofill : int

Number of bins to zero fill with.

Returns:

f : :

the center frequency of the frequencies represented in the

spectra

spectrum_water, spectrum_water_suppressed:

The first spectrum is for the data with water not suppressed and the second spectrum is for the water-suppressed data.

Notes

This function performs the following operations:

1. Filtering.

2. Apodizing/windowing. Optionally, this is done with line-broadening (see page 92 of Keeler2005. 3. Spectral analysis.

[Keeler2005]

Keeler, J (2005). Understanding NMR spectroscopy, second edition. Wiley (West Sussex, UK).

integrate

MRS.analysis.integrate(func, x, args=(), offset=0, drift=0)

Integrate a function over the domain x

Parameters:

func : callable

A function from the domain x to floats. The first input to this function has to be x, an array with values to evaluate for, running in monotonic order

x : float array

The domain over which to integrate, as sampled. This can be monotonically decreasing or monotonically increasing.

args : tuple

The parameters of func after x.

offset : :

Notes

We apply the trapezoid rule for integration here, using scipy.integrate.trapz.

See: http://en.wikipedia.org/wiki/Trapezoidal_rule

scalemodel

MRS.analysis.scalemodel(model, scalefac)

Given a scale factor, multiply by model to get scaled model

Parameters:

model : array

original model

scalefac : array of model.shape[0]

array of scalefactors

Returns:

scaledmodel : array

model scaled by scale factor

separate_signals

MRS.analysis.separate_signals(data, w_idx=[1, 2, 3])

Separate the water and non-water data from each other

Parameters:

data : nd array

FID signal with shape (transients, echos, coils, time-points)

w_idx : list (optional)

Indices into the ‘transients’ (0th) dimension of the data for the signal that is not water-suppressed

Returns:

water_data, w_supp_data : tuple

The first element is an array with the transients in the data in which no water suppression was applied. The second element is an array with the transients in which water suppression was applied

simple_auc

MRS.analysis.simple_auc(spectrum, f_ppm, center=3.0, bandwidth=0.3)

Calculates area under the curve (no fitting)

Parameters:

spectrum : array of shape (n_transients, n_points)

Typically the difference of the on/off spectra in each transient.

center, bandwidth : float

Determine the limits for the part of the spectrum for which we want to calculate the AUC. e.g. if center = 3.0, bandwidth = 0.3, lower and upper bounds will be 2.85 and 3.15 respectively (center +/- bandwidth/2).

Notes

Default center and bandwidth are 3.0 and 0.3ppm respectively

because of Sanacora 1999 pg 1045:

“The GABA signal was integrated over a 0.30-ppm bandwidth at 3.00ppm”

Ref: Sanacora, G., Mason, G. F., Rothman, D. L., Behar, K. L., Hyder, F., Petroff, O. A., ... & Krystal, J. H. (1999). Reduced cortical {gamma}-aminobutyric acid levels in depressed patients determined by proton magnetic resonance spectroscopy. Archives of general psychiatry, 56(11), 1043.

simps

MRS.analysis.simps(y, x=None, dx=1, axis=-1, even='avg')

Integrate y(x) using samples along the given axis and the composite Simpson’s rule. If x is None, spacing of dx is assumed.

If there are an even number of samples, N, then there are an odd number of intervals (N-1), but Simpson’s rule requires an even number of intervals. The parameter ‘even’ controls how this is handled.

Parameters:

y : array_like

Array to be integrated.

x : array_like, optional

If given, the points at which y is sampled.

dx : int, optional

Spacing of integration points along axis of y. Only used when x is None. Default is 1.

axis : int, optional

Axis along which to integrate. Default is the last axis.

even : {‘avg’, ‘first’, ‘str’}, optional

‘avg’ : Average two results:1) use the first N-2 intervals with

a trapezoidal rule on the last interval and 2) use the last N-2 intervals with a trapezoidal rule on the first interval.

‘first’ : Use Simpson’s rule for the first N-2 intervals with

a trapezoidal rule on the last interval.

‘last’ : Use Simpson’s rule for the last N-2 intervals with a

trapezoidal rule on the first interval.

See also

quad

adaptive quadrature using QUADPACK

romberg

adaptive Romberg quadrature

quadrature

adaptive Gaussian quadrature

fixed_quad

fixed-order Gaussian quadrature

dblquad

double integrals

tplquad

triple integrals

romb

integrators for sampled data

cumtrapz

cumulative integration for sampled data

ode

ODE integrators

odeint

ODE integrators

Notes

For an odd number of samples that are equally spaced the result is exact if the function is a polynomial of order 3 or less. If the samples are not equally spaced, then the result is exact only if the function is a polynomial of order 2 or less.

subtract_water

MRS.analysis.subtract_water(w_sig, w_supp_sig)

Subtract the residual water signal from the Normalize the water-suppressed signal by the signal that is not water-suppressed, to get rid of the residual water peak.

Parameters:

w_sig : array with shape (n_reps, n_echos, n_points)

A signal with water unsupressed

w_supp_sig :array with shape (n_reps, n_echos, n_points) :

A signal with water suppressed.

Returns:

The water suppressed signal with the additional subtraction of a scaled :

version of the signal that is presumably just due to water. :

trapz

MRS.analysis.trapz(y, x=None, dx=1.0, axis=-1)

Integrate along the given axis using the composite trapezoidal rule.

Integrate y (x) along given axis.

Parameters:

y : array_like

Input array to integrate.

x : array_like, optional

If x is None, then spacing between all y elements is dx.

dx : scalar, optional

If x is None, spacing given by dx is assumed. Default is 1.

axis : int, optional

Specify the axis.

Returns:

trapz : float

Definite integral as approximated by trapezoidal rule.

See also

sum, cumsum

Notes

Image [R2] illustrates trapezoidal rule – y-axis locations of points will be taken from y array, by default x-axis distances between points will be 1.0, alternatively they can be provided with x array or with dx scalar. Return value will be equal to combined area under the red lines.

References

[R1]	Wikipedia page: http://en.wikipedia.org/wiki/Trapezoidal_rule

[R2]	(1, 2) Illustration image: http://en.wikipedia.org/wiki/File:Composite_trapezoidal_rule_illustration.png

Examples

>>> np.trapz([1,2,3])
4.0
>>> np.trapz([1,2,3], x=[4,6,8])
8.0
>>> np.trapz([1,2,3], dx=2)
8.0
>>> a = np.arange(6).reshape(2, 3)
>>> a
array([[0, 1, 2],
       [3, 4, 5]])
>>> np.trapz(a, axis=0)
array([ 1.5,  2.5,  3.5])
>>> np.trapz(a, axis=1)
array([ 2.,  8.])